Caída de Tensión en Conductores: Cargas Distribuidas

Líneas de CA Monofásica en BT

En este primer estudio preparamos un pequeño recuerdo del cálculo de pérdidas en líneas de corriente alterna monofásica. Lo exponemos mediante ejemplos prácticos, con su desarrollo matemático, pues creemos que esta es la forma más ágil e intuitiva de proporcionar conocimientos teóricos. Y para hacerla un poco más interesante, nos saltamos los archiconocidos ejemplos que se refieren a una línea, o tramo de línea, con una sola carga en su extremo, y nos enfocamos en ejemplos con cargas distribuidas a diferentes distancias de una línea principal, en la cual nos interesa calcular pérdidas de tensión.

Como complemento, al final de la publicación, dejamos un enlace para la descarga de una sencilla planilla Excel que fue diseñada tomando en cuenta los conocimientos expuestos a continuación. Es un programa simple para encontrar la caída de tensión en una línea principal de sección constante o telescópica, con carga distribuida o agrupada en un extremo, y para conductores de cobre o aluminio. 

Finalmente, cabe recordar que la elección definitiva del conductor, para una aplicación práctica, deberá considerar no solo sus pérdidas de energía, sino también su capacidad para transportar la corriente del consumo sin exceder sus temperaturas de servicio; su capacidad para soportar los requerimientos que le imponga el sistema en condiciones de falla; y sus condiciones de instalación, las cuales deben asegurar su integridad mecánica y eléctrica.

Bases para el cálculo

Es sabido que al circular corriente por los conductores de una línea se producirá una caída de tensión en ellos, u, expresada como:

u = 2 I l    (Volts)  de donde  s = 2 I l    (mm2)
        ϒ s                                      ϒ u                                                    

Con carga inductiva interviene el factor de potencia, por tanto

s =  2 l I cos φ  (mm2)

           ϒ u 

y si la carga viene expresada en Watts

s =  2 P l     (mm2)

      ϒ u U

en todas ellas: I es la intensidad, en Ampers, que circula por los conductores; l la longitud sencilla de la línea, en metros; ϒ es la conductividad eléctrica específica (para el cobre, 56; para el aluminio, 35); U es la tensión de servicio en Volts; P es la potencia de la carga expresada en Watts; y s es la sección del conductor que se calcula en mm2. 

Estás fórmulas se refieren a una línea con una sola carga en su final, ahora veremos las ecuaciones para líneas con varias cargas a diferentes distancias.

Líneas con cargas no Inductivas

Ejemplo n°1. Calcular la sección de la línea de cobre de la figura (representación unipolar). La carga está indicada en Ampers, y el cos φ = 1. La caída de tensión no debe pasar de un 3% de la tensión de bornes de 220 (Volts).

Formula a emplear:

s =   2   ∑(i l cos φ)   (mm2)                                                                

       ϒ u                                             

La caída de tensión expresada en Volts:

u =   up x U   (Volts) = 3 x 220 = 6,6 (Volts)

         100                        100

∑(i l cos φ) =  

30 x  60 x 1  =   180

20 x 100 x 1 =   200

10 x 150 x 1 = 1500

                       5300

                                                   

s =      2       x 5300 = 28,7(mm2)
       56 x 6,6

La sección comercial más próxima es la de 35(mm2) o 2 AWG. La carga total vale 30 + 20 + 10 = 60 (A).

Líneas con cargas Inductivas

Ejemplo n°2. Determinar la sección de la línea de la figura cuya caída de tensión no debe exceder del 5%. La tensión de servicio es de 220 (Volts).

Para tener las tres cargas en Watts, calcularemos la potencia de la carga de 30(A).

P = i U cos φ = 30 x 220 x 0,8 = 5300 (Watts)

Formula a emplear:

s =      2     ∑(P l)  (mm2)

       ϒ u U 

el 5% de la tensión es 11 (Volts), entonces:
                                                                                   

∑(P l) =   

5300   x   80 =   425000
10000 x 120 =  1200000
20000 x 180 =  3600000
                           5225000

s =          2         x 5225000 = 77,1 (mm2) 
      56 x 11 x 220

La sección comercial más próxima es de 95 (mm2) o 3/0 AWG. La carga total vale:

I = i1+i2+i3 = 30 +    10000     + 20000 = 186(A)
                                 220 x 0,7      220

Líneas con cargas uniformemente repartidas
Es el caso, por ejemplo, de una línea larga con muchas luminarias equidistantes, aunque también puede aplicarse en líneas con muchas derivaciones y que para mayor facilidad se supone que las cargas están repartidas uniformemente.

Se puede deducir, en base al cálculo integral, que esta configuración de consumos se comporta como si toda la carga estuviese concentrada en el centro de la línea. Y si la carga está indicada en Ampers, la fórmula es,

s =    2     I    l     (mm2)
       56 u       2 

Donde I  es la carga total.

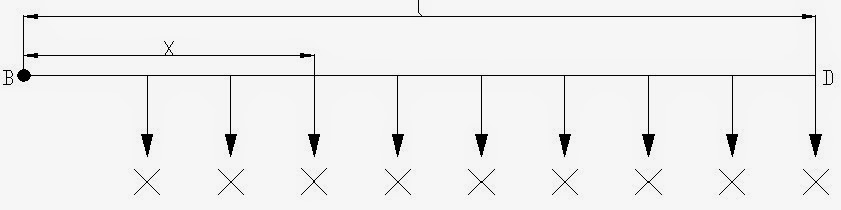
Ejemplo n°3. Determinar la sección de una línea de 200 metros de longitud que a cada 10 metros alimenta 2 luminarias de 60(Watts). La caída de tensión no debe exceder del 4% y la tensión de servicio es de 220 (Volts).

El número total de equipos de alumbrado será:

n =  200  x 2 = 40 Luminarias

         10

y su potencia y carga total,

P = 40 x 60 = 2400 (Watts)   I = 2400 = 10,9 (Ampers)

                                                   220 

El 4% de la tensión es 8,8 (Volts), entonces la sección

s =     2      x 10,9 x 200 = 4,4 (mm2)

        56 x 8,8              2

La sección comercial más próxima es la de 6(mm2) o 10 AWG.

Líneas con sección telescópica o cónica

Son las líneas en las que su sección va decreciendo en cada uno de los tramos a medida que nos alejamos del punto de alimentación. 

Ejemplo n°4. Determinar la sección de la línea de la figura, para que la densidad de corriente, d, que circula por ella sea la misma en todos los tramos y la pérdida de tensión total no supere el 3%. La tensión de servicio es de 220 (Volts).
Formulas a emplear:

d =  u ϒ   (Ampers/mm2)        sn = In /d (mm2)

        2 l               

el 3% de la tensión es 6,6 (Volts) y el largo total de la línea es de 90(metros)

d =   6,6 x 56    = 2,1 (Ampers/mm2)

           2 x 90 

I1 = 15+22+18 = 55 (Ampers)
      

I2 = 22+18 = 40 (Ampers)

I3 = 18 (Ampers)

sn1 = 55  = 26,2 (mm2);  sn2 = 40  = 19,1 (mm2);  sn3 = 18  = 8,6 (mm2)
        2,1                                   2,1                                  2,1 
         

Las secciones normalizadas serán 26,7(mm2), 21,15(mm2) y 10(mm2).



Caída de Tensión en Conductores: Cargas Distribuidas II

Descarga en Scribd
Programa de cálculo de caída de tensión
Descarga en Box
Programa de cálculo de caída de tensión

Referencias
1.-Instalaciones de baja tensión Calculo de líneas eléctricas. Enciclopedia CEAC.
2.-Introducción Al Proyecto Eléctrico. Jorge Valenzuela Alvarado.